Publications
You can welcomely find my articles on my Google Scholar profile or arXiv.
Selected Works
Model-independent Direct Extraction of the Central Neutron Star Equation of State
Understanding the extreme physical conditions inside neutron stars is a major challenge in modern nuclear astrophysics. A key difficulty lies in the large theoretical uncertainty of the equation of state of dense matter, which governs how pressure and energy density relate deep within these compact stars. In this work, we introduce IPAD-TOV (Intrinsic and Perturbative Analyses of the Dimensionless Tolman-Oppenheimer-Volkoff equations), a novel reformulation of the TOV equations that describe hydrostatic equilibrium in general relativity. By expressing the TOV equations in a dimensionless form, IPAD-TOV uncovers nearly universal relations among core quantities such as pressure, energy density, and sound speed, relations that remain robust across a wide range of equation of state models. This framework enables a model-independent anatomical study of neutron star interiors, allowing key core properties to be inferred directly from observations. By linking global observables to microphysical insights, IPAD-TOV provides a powerful new tool to constrain the behavior of strongly interacting matter in one of nature’s most extreme environments. For details, see our paper 1 and paper 2, and related paper 3, paper 4, paper 5 and paper 6.
\[\mathcal{U}/\mathcal{U}_{\rm{c}}=1+\sum_{i+j\geq1}^{\infty}u_{ij}\mu^i{\rm X}^j\] \[M_{\rm{NS}}\sim \frac{\Pi_{\rm{c}}^{3/2}}{\sqrt{\varepsilon_{\rm{c}}}},R\sim \frac{\Pi_{\rm{c}}^{1/2}}{\sqrt{\varepsilon_{\rm{c}}}},\Pi_{\rm{c}}=\frac{\rm X}{1+3{\rm X}^2+4{\rm X}},{\rm X}=P_{\rm{c}}/\varepsilon_{\rm{c}}\]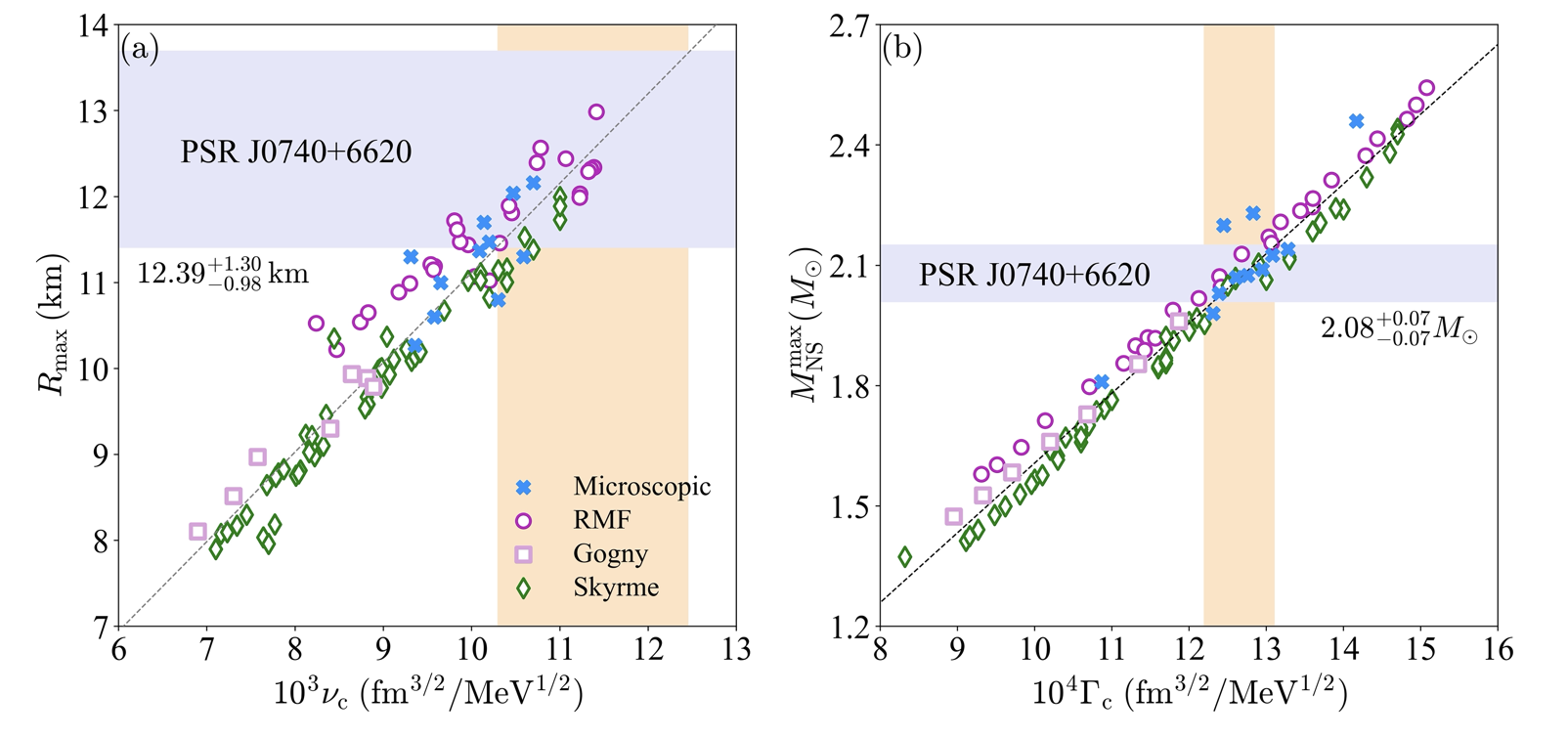
Data-driven Bayesian Model Averaging for Nuclear Symmetry Energy Constraints
This project applies a data-driven Bayesian model averaging framework to constrain the nuclear symmetry energy at subsaturation densities. Bayesian model averaging (BMA) is a rigorous statistical approach that integrates predictions from multiple theoretical models, yielding more robust estimates in the presence of model-dependent uncertainties. By analyzing the effective proton-neutron chemical potential differences in several neutron-rich doubly magic nuclei, the study identifies a strong sensitivity to the symmetry energy around two-thirds of nuclear saturation density. Using Gaussian process emulators trained on both Skyrme energy density functionals and relativistic mean field models, the symmetry energy in this density region is inferred with reduced theoretical bias. The extracted result aligns well with predictions from microscopic theories and other empirical indicators, demonstrating the effectiveness of BMA in improving the reliability of nuclear matter constraints. For details, see this paper.
\[p(\mathcal{O}|\mathbf{y})=\sum_{i=\rm{models}}p(\mathcal{O}|\mathbf{y},\mathcal{M}_i)p(\mathcal{M}_i|\mathbf{y})\]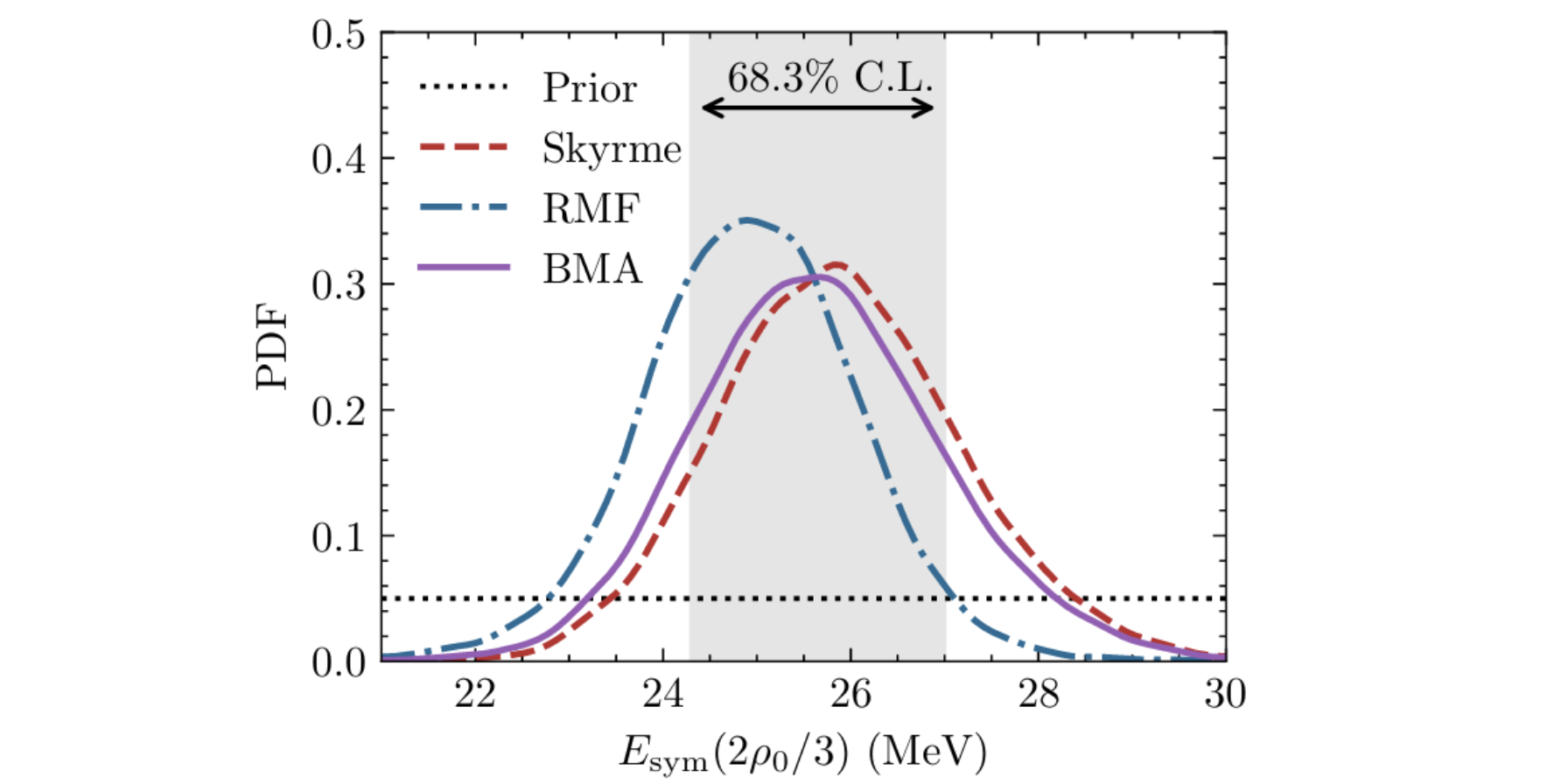
Implications of the Non-existence of a Surface in Nuclear Matter
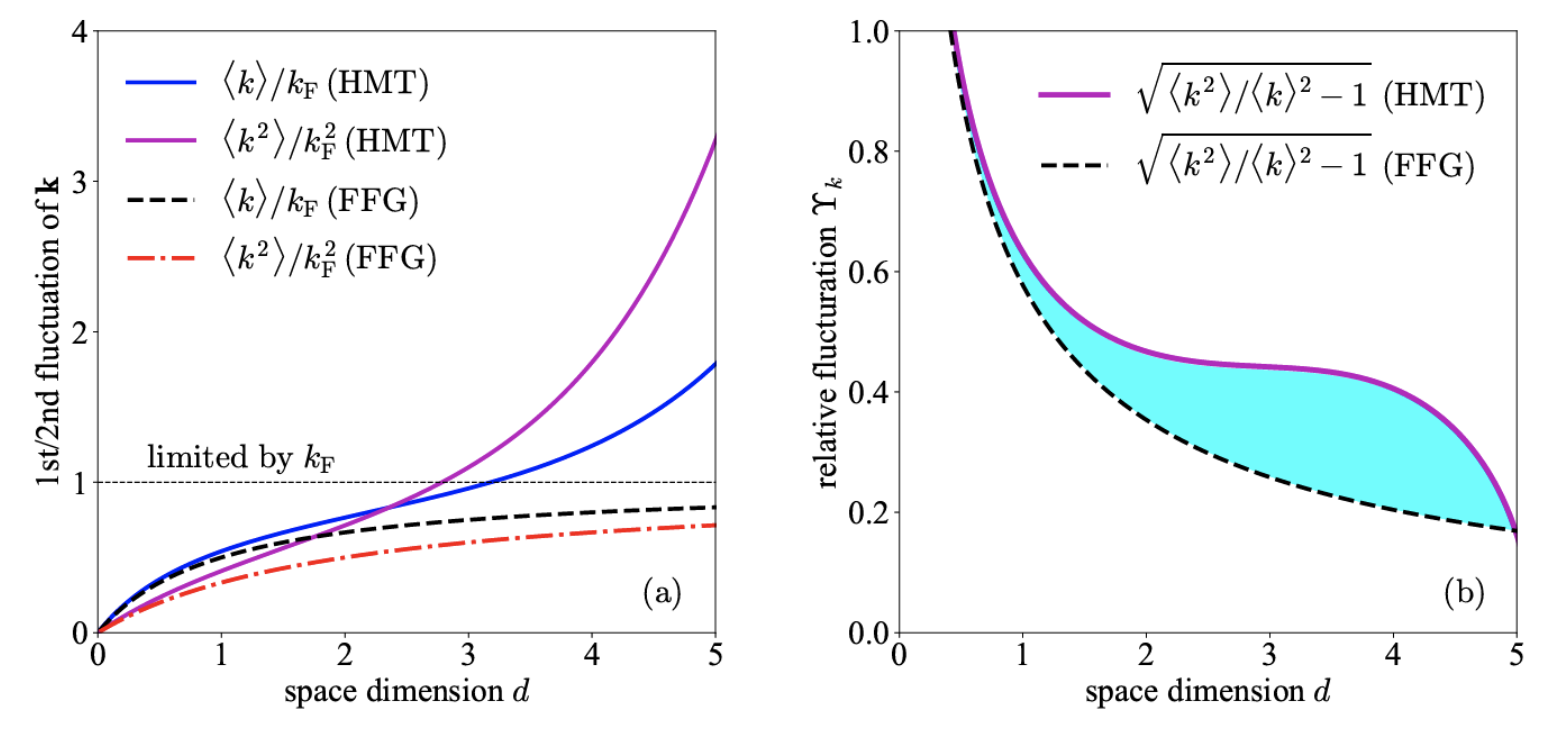
This work revisits the connection between the fourth-order symmetry energy of infinite nuclear matter at saturation density and its counterpart in finite nuclei within the semiempirical nuclear mass formula framework. By explicitly incorporating high-order isospin-dependent surface tension effects, we derive a complete expression for the finite-nucleus fourth-order symmetry energy. We demonstrate that extracting the nuclear matter fourth-order symmetry energy from finite nuclei data requires precise knowledge of these surface tension contributions. Our findings reconcile previously conflicting large values of finite-nucleus symmetry energy with empirical constraints from mean-field models, showing that ignoring high-order surface tension can significantly overestimate the nuclear matter parameter. Additionally, we provide the expression for the sixth-order symmetry energy of finite nuclei, which depends on more bulk nuclear matter parameters and higher-order surface tension effects. For details, see this paper.
\[a_{\rm{sym,4}}^{\rm{s}}(A)=\frac{4\alpha^4\theta\kappa}{\beta A^{1/3}}\cdot(1+\alpha/\beta A^{1/3})^{-4}\]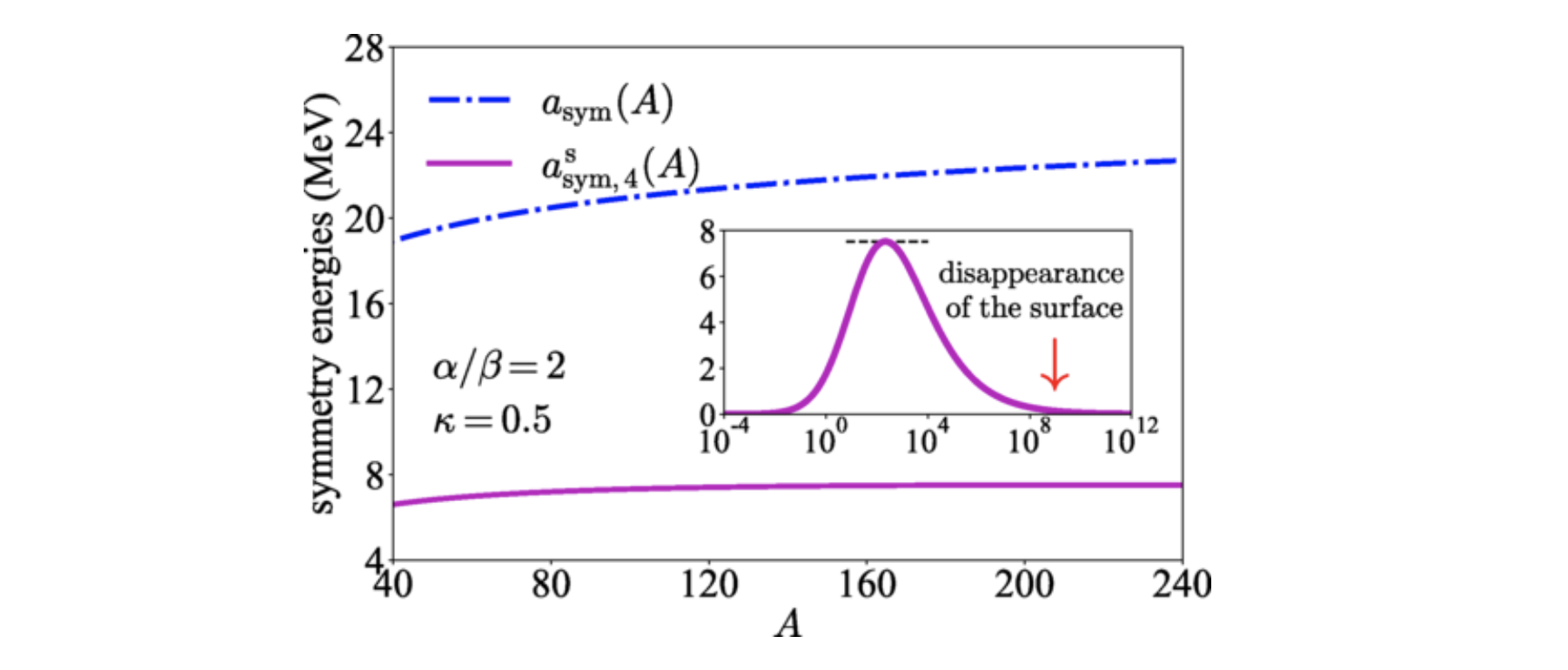
Equation of State of Nuclear Matter in Arbitrary Spatial Dimensions
This work generalizes the Hugenholtz–Van Hove theorem to arbitrary spatial dimensions and derives analytical expressions for the equation of state of asymmetric nuclear matter across different dimensional settings. By systematically analyzing the behavior of key nuclear matter properties, such as pressure, incompressibility, and symmetry energy, in reduced or increased spatial dimensions, the study reveals that nuclear systems become more tightly bound and the symmetry energy generally decreases in lower-dimensional spaces. The parabolic approximation remains robust, supported by the suppressed role of higher-order terms across dimensions. An epsilon-expansion framework, based on perturbations around the conventional 3D case, enables tractable connections between the equation of state in 3D and its counterparts in nearby dimensions. A phenomenological model consistent with empirical nuclear and astrophysical constraints is constructed to investigate these effects in detail. The findings indicate that systems in low dimensions often behave like nearly free Fermi gases, especially when short-range correlations are included, while higher-dimensional cases can exhibit unbound behavior. These insights not only offer new perspectives on the dimensional dependence of strongly interacting matter but also have potential implications for modeling exotic nuclear systems, emergent few-body structures, and the behavior of dense matter in astrophysical environments. For details, see this paper.
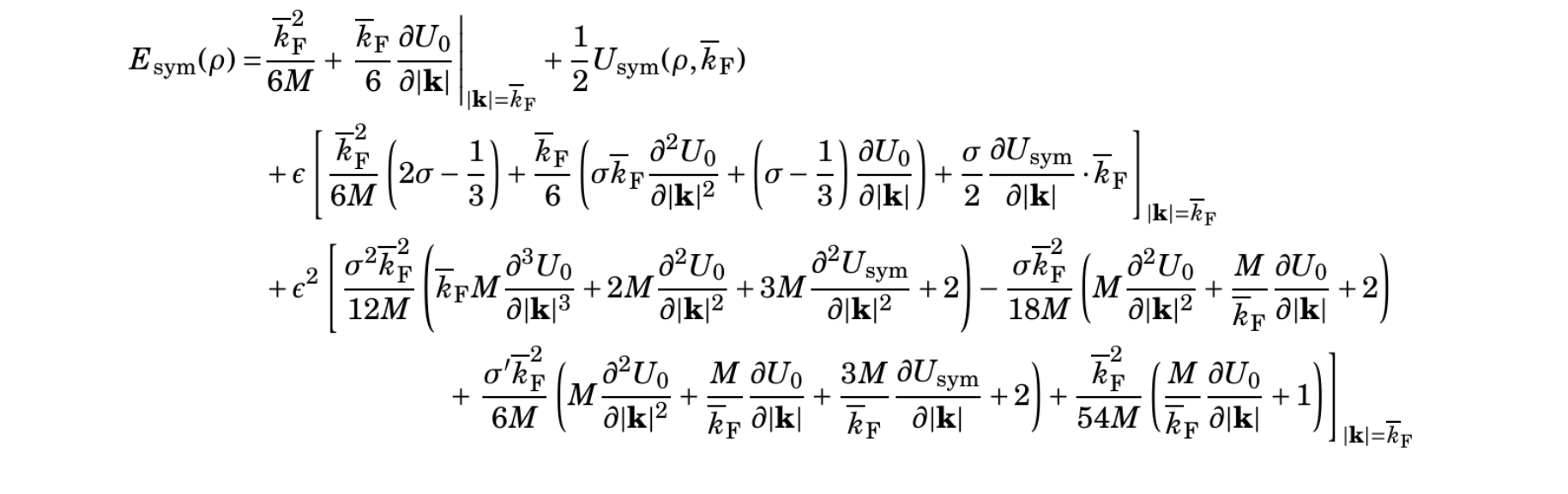
What Does the Absence of Saturation Density in Pure Neutron Matter Imply?
This project investigates the intrinsic correlations between the equation of state parameters of symmetric nuclear matter and the nuclear symmetry energy, based on the fundamental physical constraint that pure neutron matter is unbound in nature that is, it does not saturate at any finite density and continues to lower its energy as the density decreases. By expressing the energy per nucleon of neutron-rich matter as a power series in isospin asymmetry, an analytical condition is derived from setting the saturation density of pure neutron matter to zero. This leads to sum rules that link key symmetry energy parameters, such as its slope, curvature, and skewness, to better-determined parameters of symmetric nuclear matter, such as incompressibility, skewness, and kurtosis. These model-independent correlations reproduce trends observed in various microscopic and phenomenological studies, offering a powerful tool to constrain the poorly known high-density behavior of nuclear symmetry energy using more reliably known properties of symmetric matter. For details, see this paper.
\[L\approx\frac{K_0}{3}\cdot(1+\textrm{''corrections''})\]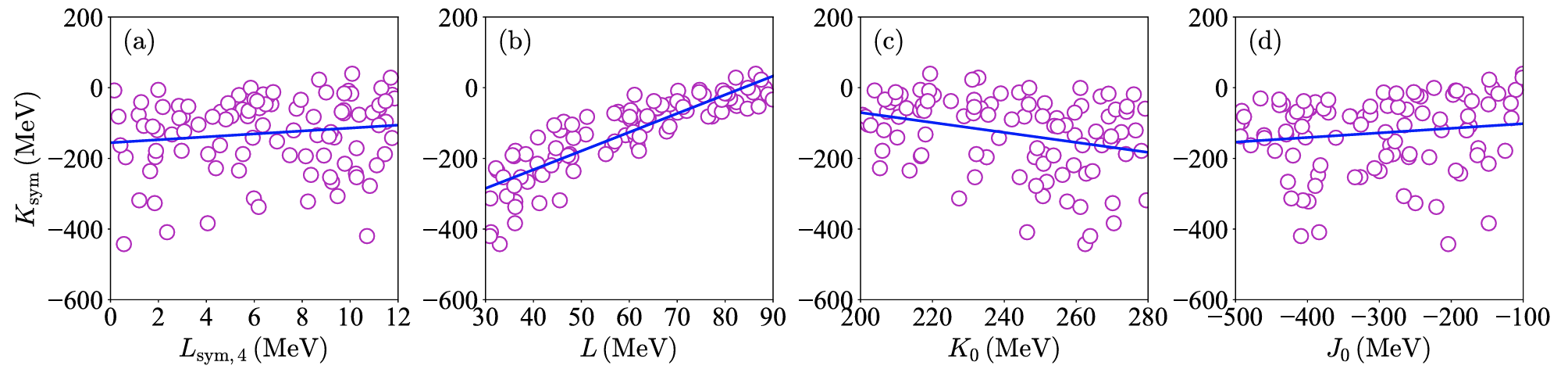
Neutron and Nuclear Matter Probed by QCD Sum Rules
This project investigates the low-density equation of state of isospin-asymmetric nuclear matter using QCD sum rules, providing a connection between nuclear matter properties and the underlying quark and gluon dynamics. Based on the Hugenholtz–Van Hove theorem, the approach enables the derivation of analytical expressions for key quantities such as the energy per particle, pressure, and symmetry energy, grounded in fundamental QCD condensates. By incorporating inputs from nuclear experiments and astrophysical observations, the framework constrains the in-medium behavior of quark and gluon condensates and offers insight into hadronic modifications and partial chiral symmetry restoration. Special attention is given to the treatment of four-quark condensates, which are modeled through effective interpolation but play a non-negligible role in theoretical uncertainties. The use of complex-valued Borel transformations helps improve the resolution of spectral functions, extending the applicability of the method. Low-density neutron matter, with its near-universal behavior similar to a unitary Fermi gas, provides a compelling testing ground for these calculations, particularly for extracting imaginary parts of self-energies and transport coefficients through other advanced techniques. For details, see our paper 1 and paper 2.
\[E_{\rm{n}}(\rho) \approx E_{\rm{n}}^{\rm{FFG}}(\rho)-\frac{\rho}{2}\frac{m_{\rm{n}}}{\langle\overline{q}q\rangle_{\rm{vac}}}(5-{\sigma_{\rm{N}}}/{2m_{\rm{q}}})\]
Protons Move Faster than Neutrons in Skins of Neutron-rich Nuclei
This project explores the dual manifestation of neutron skins in coordinate space and proton skins in momentum space in heavy nuclei. Governed by Liouville’s theorem and Heisenberg’s uncertainty principle, the coexistence and correlation of these spatial and momentum distributions are investigated within an extended Thomas-Fermi approximation, which is a model-independent semiclassical framework. This approach incorporates the effects of nucleon short-range correlations, capturing universal features of finite nuclear systems without reliance on specific interaction models. A key physical insight lies in the high-momentum tail of the nucleon momentum distribution, induced by short-range correlations and characterized by a pronounced isospin dependence, favoring proton enrichment at high momenta in neutron-rich systems. This mechanism underlies the robust finding that, in nuclei with neutron-rich surfaces, protons tend to exhibit higher average momenta than neutrons. The study offers a new lens through which to view the internal dynamics of asymmetric nuclei and sheds light on the fundamental interplay between spatial and momentum distributions. For details, see this paper.
\[n_{\mathbf{k}}\sim\psi^2(\mathbf{k})\to\frac{C}{|\mathbf{k}|^4},~~|\mathbf{k}|\to\infty\]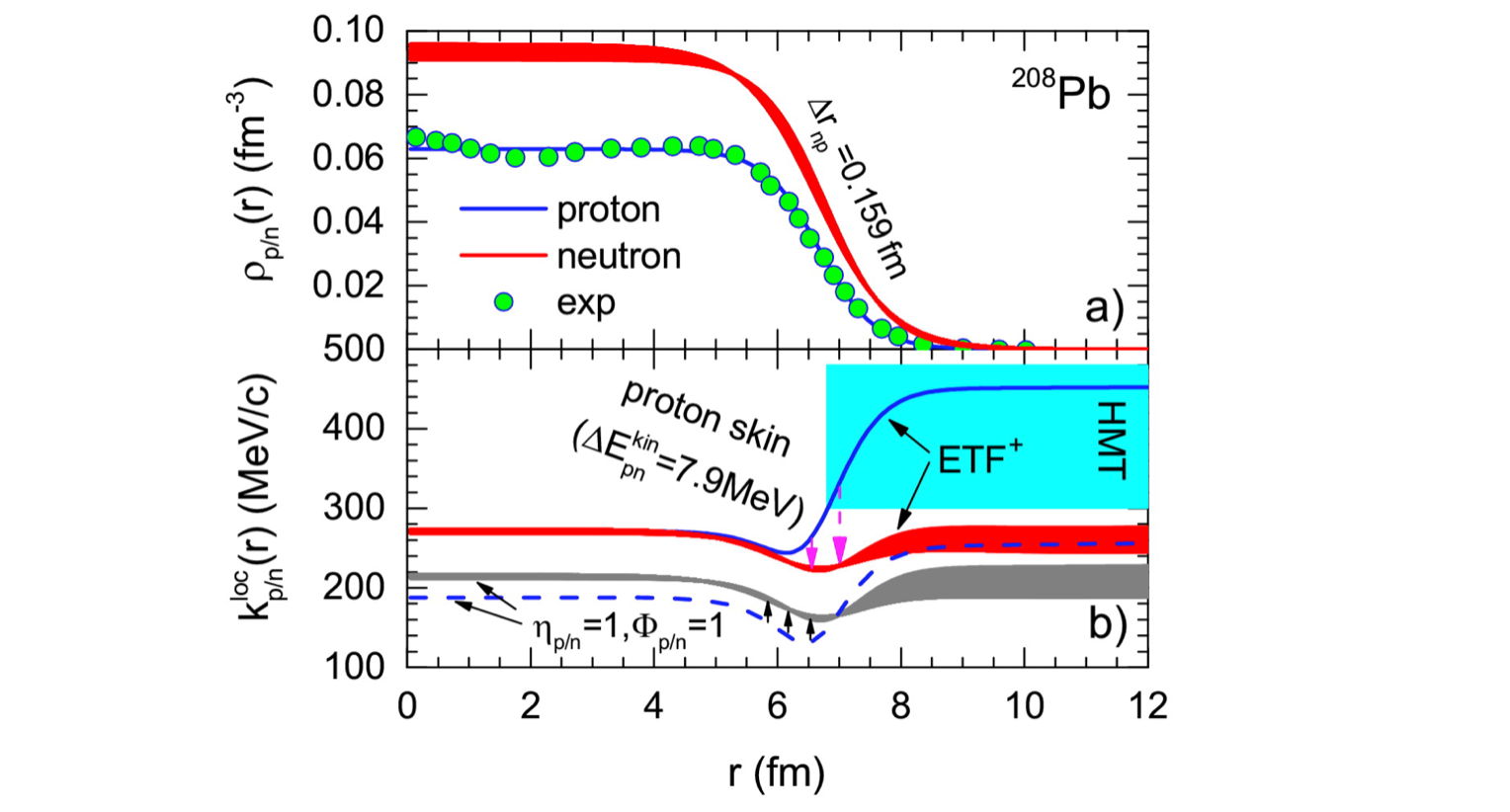
Softening of Nuclear Symmetry Energy due to Isospin-dependent Nucleon-nucleon Short-range Correlations
This project explores the impact of nucleon-nucleon short-range correlations, which stem from the strongly isospin-dependent nuclear tensor force. These correlations significantly enhance the interaction between neutron–proton pairs compared to like-nucleon pairs, leading to a redistribution of nucleons in momentum space: a larger fraction of protons are promoted to high-momentum states above the Fermi surface in neutron-rich matter. This isospin-dependent modification of the nucleon momentum distribution has profound implications. One of the most important is its softening effect on the nuclear symmetry energy, particularly at supra-saturation densities. The symmetry energy, which quantifies the energy cost of converting protons into neutrons in nuclear matter, becomes less stiff due to the increased high-momentum content of protons relative to neutrons. This softening has consequences for the structure of neutron-rich nuclei and the properties of dense astrophysical objects like neutron stars. The phenomenon is investigated within a modified Gogny–Hartree–Fock energy density functional that incorporates the high-momentum tail of the nucleon momentum distribution, allowing for a detailed and physically grounded analysis. For details, see our paper 1 and paper 2.
\[E_{\textrm{sym}}(\rho)\approx E_{\textrm{n}}(\rho)-E_{\textrm{0}}(\rho)\]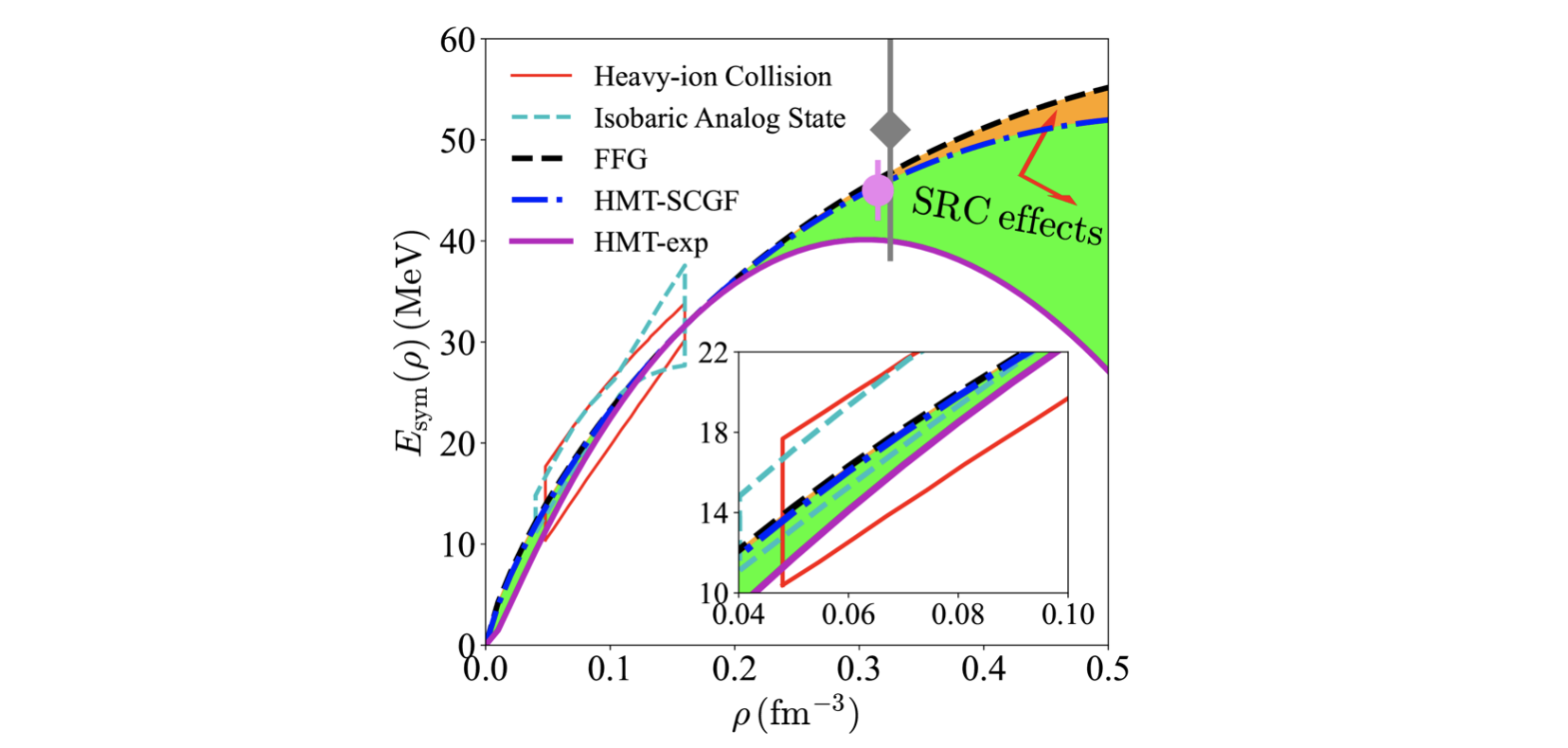
Role of High-momentum Nucleons in Neutron Star Equation of State and Mass Limit
Short-range nucleon-nucleon correlations strongly modify the single-nucleon momentum distribution in neutron-rich matter, creating a high-momentum tail that significantly impacts the equation of state. Incorporating these effects into a nonlinear relativistic mean field model reveals important consequences for neutron stars. The high-momentum nucleons increase the kinetic pressure at densities above nuclear saturation, which in turn enhances the maximum mass that neutron stars can support. Additionally, the short-range correlations soften the density dependence of the nuclear symmetry energy around saturation density, making it more concave at both lower and higher densities. This softening leads to an isospin-dependent incompressibility of asymmetric nuclear matter that aligns better with experimental data and influences neutron star structure and stability. Overall, considering nucleon-nucleon short-range correlations provides a more realistic description of dense matter inside neutron stars and helps explain observed neutron star masses. For details, see this paper.
\[{\int_0^{k_{\textrm{F}}^J}\overbrace{(\textrm{FFG step function})}^{\Theta(k_{\textrm{F}}^J-|\mathbf{k}|)}s(\mathbf{k},\rho,\delta)\textrm{d}\mathbf{k}\to\int_0^{\phi_Jk_{\textrm{F}}^J}n_{\mathbf{k}}^J(\textrm{HMT})s(\mathbf{k},\rho,\delta)\textrm{d}\mathbf{k}}\]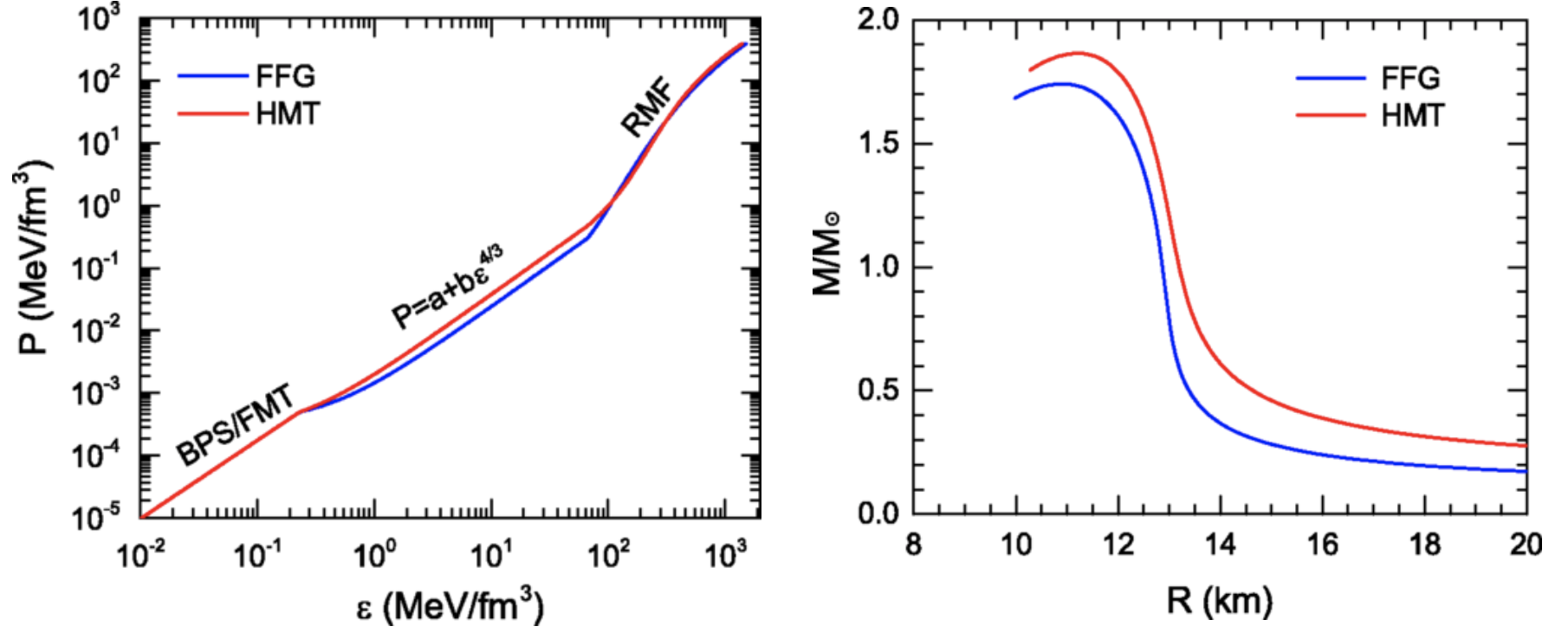
Significant Quartic and Negative Quadratic Terms in the Kinetic Energy of Neutron-rich Matter from Isospin-dependent Nucleon Momentum Distribution
This work reveals that, contrary to the nearly parabolic approximation commonly assumed, the kinetic energy of interacting nucleons in neutron-rich matter contains a sizable negative quadratic term and a significant quartic term. By incorporating isospin-dependent single-nucleon momentum distributions characterized by both a low-momentum depletion and a high-momentum tail, constrained by recent experiments and advanced many-body calculations, the quartic contribution is found to be substantial. These findings have important implications for accurately determining the equation of state of neutron-rich nucleonic matter and impact the interpretation of nuclear reaction data as well as the structure and behavior of neutron stars. For details, see our paper 1 and paper 2.
\[E^{\textrm{kin}}(\rho,\delta)=\frac{1}{\rho}\underbrace{\frac{2}{(2\pi)^3}\sum_{J=\rm{n,p}}\int_0^{\infty} \frac{\mathbf{k}^2}{2M}n_{\mathbf{k}}^J(\rho,\delta)\textrm{d}\mathbf{k}}_{\textrm{kinetic energy density }\varepsilon^{\textrm{kin}}(\rho,\delta)}\]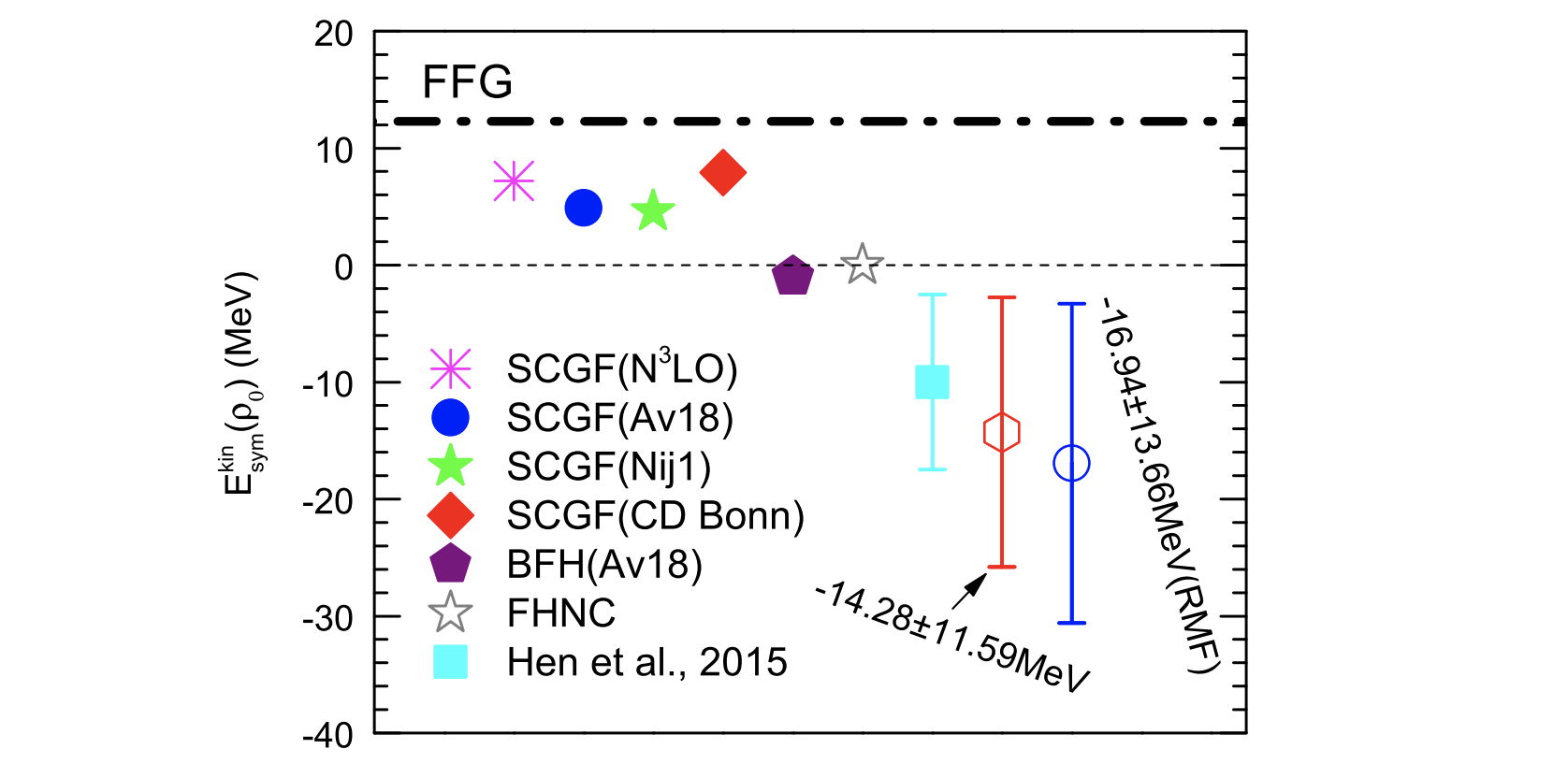
Do Delta Resonance States Appear Early in Neutron Stars?
This project investigates the critical densities for the formation of Δ(1232) resonances in neutron stars using an extended nonlinear relativistic mean-field model. The onset densities of the four Δ charge states exhibit distinct sensitivities to the kinetic and potential components of the nuclear symmetry energy, marking the first microphysical property of neutron stars shown to depend differently on these components. Additionally, the critical densities strongly depend on the in-medium Δ mass and the poorly known Δ–rho meson coupling strength. Assuming universal baryon-meson couplings, the earliest appearance of Δ(1232) occurs around twice the nuclear saturation density. The study further reveals that both the composition and the mass-radius relation of neutron stars vary significantly with these Δ-related parameters, highlighting the importance of Δ resonances in dense matter astrophysics. For details, see this paper.
\[\Delta^-+\rm{p}\to\rm{n}+\rm{n}\]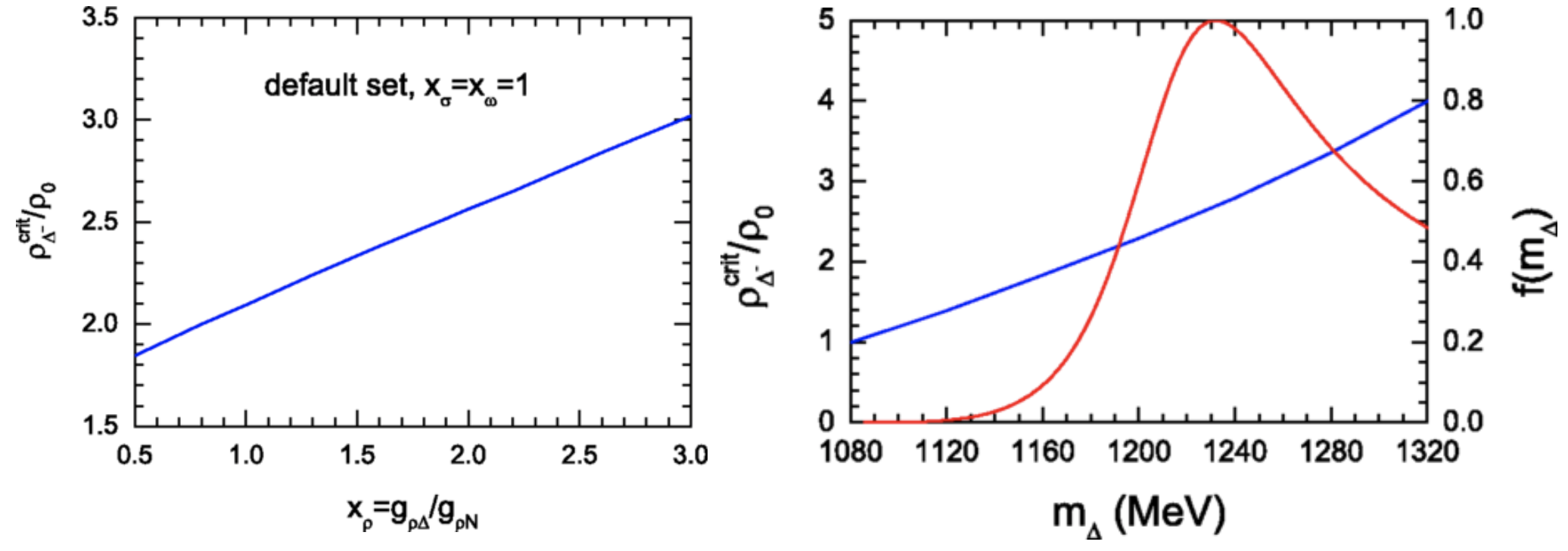
Lorentz Covariant Self-energy Decomposition of Nuclear Symmetry Energy
This project utilizes the Hugenholtz–Van Hove theorem to derive analytical expressions for the nuclear symmetry energy and its density slope in terms of Lorentz covariant nucleon self-energies in isospin asymmetric nuclear matter. These model-independent formulations provide key insights into the density dependence and microscopic origin of the symmetry energy within a fully relativistic framework. As an illustrative case, the decomposition of self-energies is analyzed in the nonlinear scalar-vector-isovector-scalar (commonly denoted as sigma–omega–rho–delta) relativistic mean-field model, where closed-form expressions are obtained. The results clarify how specific meson-nucleon couplings and Lorentz structures shape the behavior of the symmetry energy, contributing to a deeper theoretical understanding of isospin effects in dense nuclear matter. For details, see this paper.
\[E_{\rm{sym}}(\rho)=\frac{k_{\rm{F}}^2}{6E_{\rm{F}}^{\ast}}+\frac{\Sigma_{\rm{S}}^{\rm{sym}}(\rho,k_{\rm{F}})}{2}\frac{M_0^{\ast}}{E_{\rm{F}}^{\ast}}+\frac{\Sigma_{\rm{V}}^{\rm{sym}}(\rho,k_{\rm{F}})}{2}\]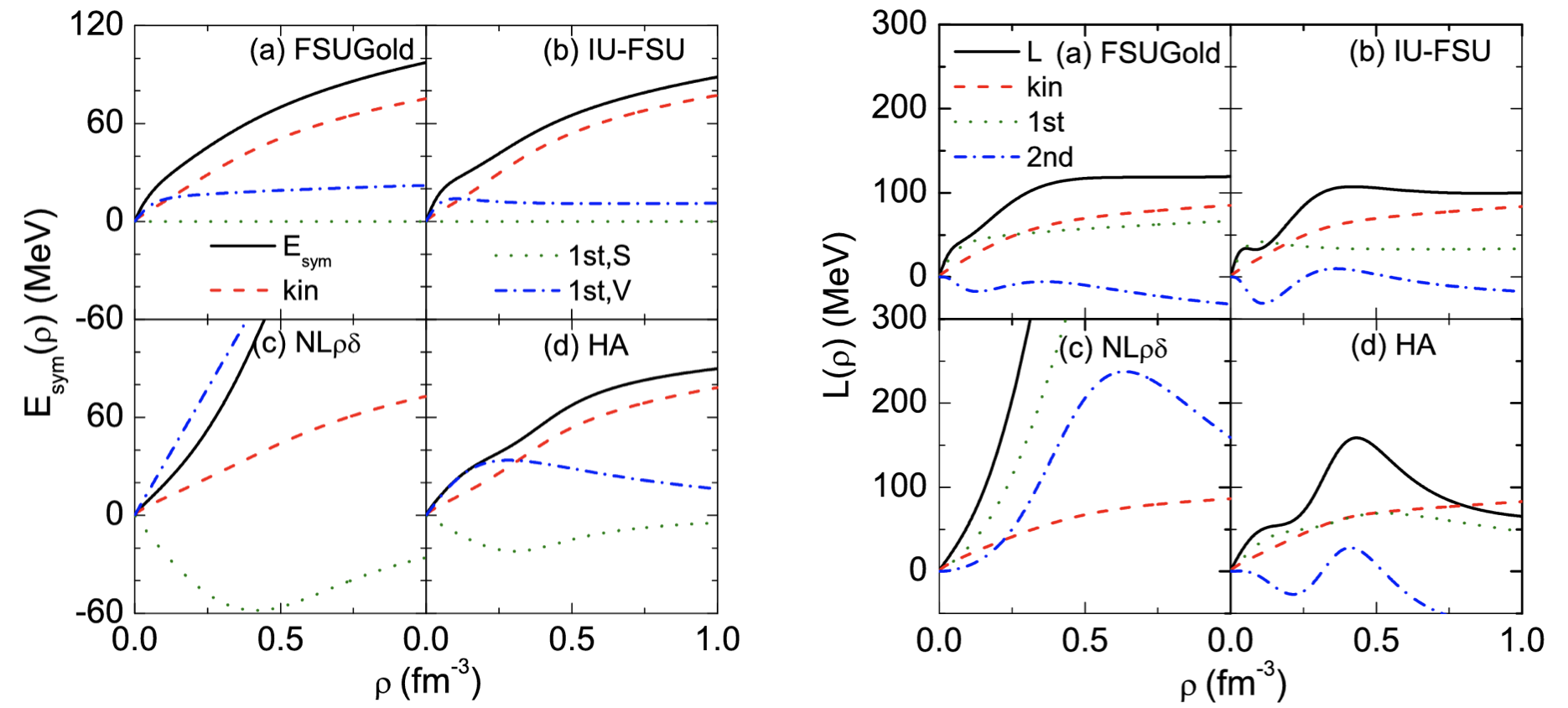
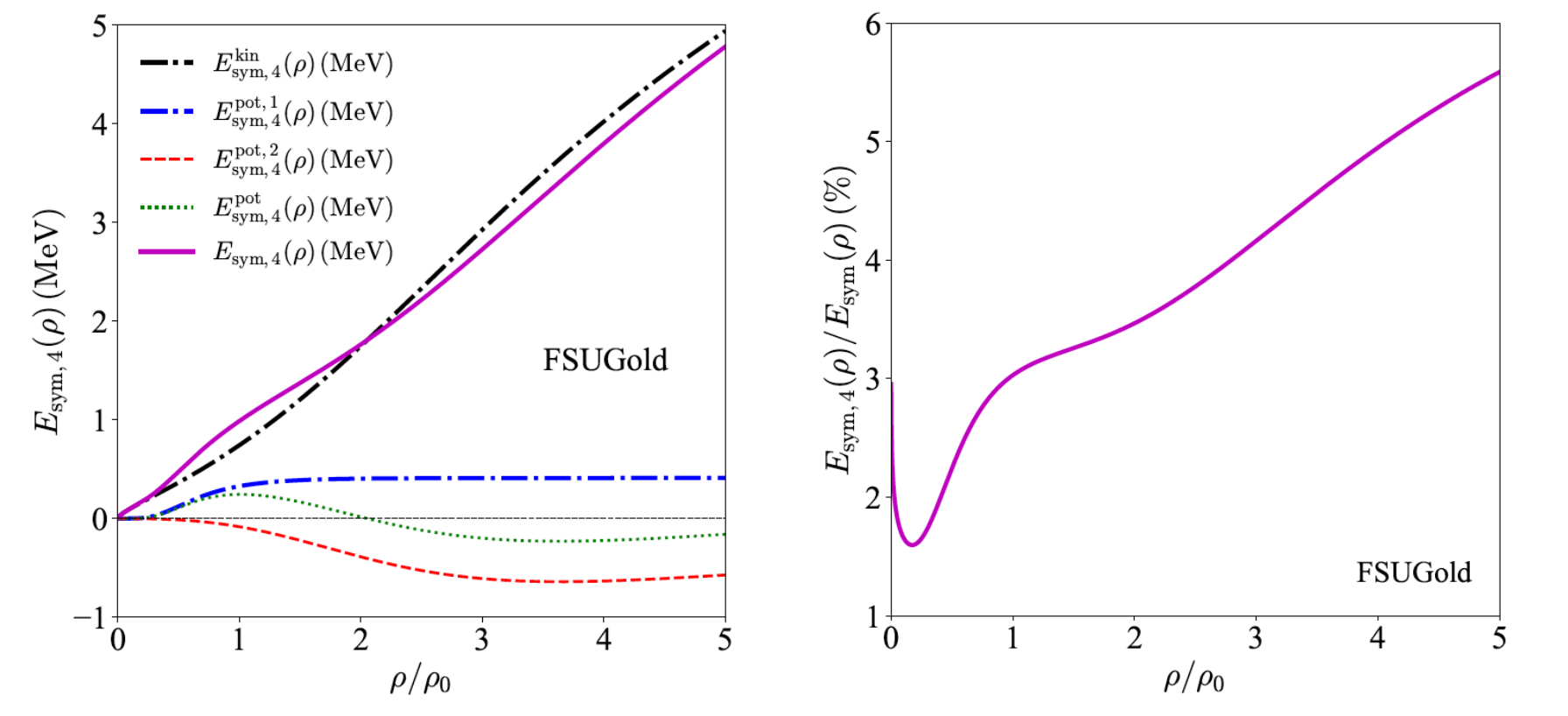
Unveiling Fourth-order Symmetry Energy in Relativistic Nuclear Matter and Neutron Stars
Within the nonlinear relativistic mean-field model, an analytical expression for the fourth-order nuclear matter symmetry energy is derived. Using two accurately calibrated interactions, FSUGold and IU-FSU, the fourth-order symmetry energy at normal nuclear matter density is found to be generally below 1 MeV, confirming the empirical parabolic approximation’s validity near saturation density. However, at higher densities, this fourth-order term becomes non-negligible. The derived expression enables a detailed study of higher-order effects on the isobaric incompressibility of asymmetric nuclear matter, showing that the fourth-order incompressibility term is generally small compared to the quadratic term. Importantly, incorporating the fourth-order symmetry energy significantly increases the proton fraction and reduces the core-crust transition density and pressure in neutron stars compared to calculations relying solely on the empirical parabolic approximation. These findings highlight potential large errors when neglecting higher-order symmetry energy contributions in modeling neutron star interiors within this relativistic framework, consistent with prior nonrelativistic results. For details, see this paper.
\[E_{\rm{sym,4}}(\rho)=24^{-1}[{\partial^4E(\rho,\delta)}/{\partial\delta^4}]_{\delta=0}\]