Our group investigates the fundamental properties of strongly interacting quantum many-body systems, with a particular emphasis on nuclear matter across diverse physical regimes. Our research spans from the microscopic structure of nuclei, such as short-range correlations and isospin-dependent dynamics in exotic nuclei, to the behavior of superdense matter created in relativistic heavy-ion collisions and residing in the cores of neutron stars under intense gravitational and magnetic fields. A central theme of our work is understanding how matter behaves under varying density, temperature, isospin asymmetry, magnetic fields, and spatial dimensions, using these extreme environments as natural laboratories to probe the non-perturbative sector of Quantum Chromodynamics (QCD). To achieve this, we develop and apply a range of effective theories and tools rooted in QCD principles, including Quantum Hadrodynamics (QHD) and QCD sum rules, the latter providing a powerful semi-analytic bridge between QCD and hadronic observables through the operator product expansion and condensate dynamics. We also explore the universality of quantum many-body behavior, drawing deep conceptual parallels between nuclear systems and ultracold atomic gases, particularly in the context of high-momentum tails and scale-invariant phenomena. Beyond traditional theory, our group actively integrates high-performance computing, large-scale optimization, and advanced machine learning algorithms to model complex systems, perform data-driven inference, and accelerate discovery. Through this multidisciplinary approach, we aim to connect the microphysics of the strong force with macroscopically observable properties of matter in nuclei, astrophysical objects, and quantum fluids—pushing the boundaries of our understanding of strongly interacting matter from femtometer to astrophysical scales.
Nucleon-nucleon Short Range Correlations
Nucleon-nucleon short range correlations (NN-SRCs) refer to the phenomenon where two nucleons inside a nucleus form tightly correlated pairs due to strong interactions at short distances, leading to high-momentum components in the nuclear wave function. About 20-25% of nucleons participate in such correlations, with a strong dominance of proton–neutron pairs. NN-SRC generate a characteristic high-momentum tail in the single-nucleon momentum distribution, which significantly deviates from traditional independent-particle models. These correlations play a pivotal role in several areas of nuclear and particle physics, e.g., they affect neutrino–nucleus interactions by altering final-state nucleon emission and impacting neutrino energy reconstruction; they provide crucial input for understanding the equation of state in heavy-ion collisions and the behavior of superdense matter in neutron stars; and they offer fundamental insight into the non-perturbative regime of the strong nuclear force beyond simple mean-field approximations. As such, NN-SRC connect low-energy nuclear structure with high-energy astrophysical phenomena and neutrino physics. Figure taken from O. Hen et al., RMP, 89, 045002 (2017).
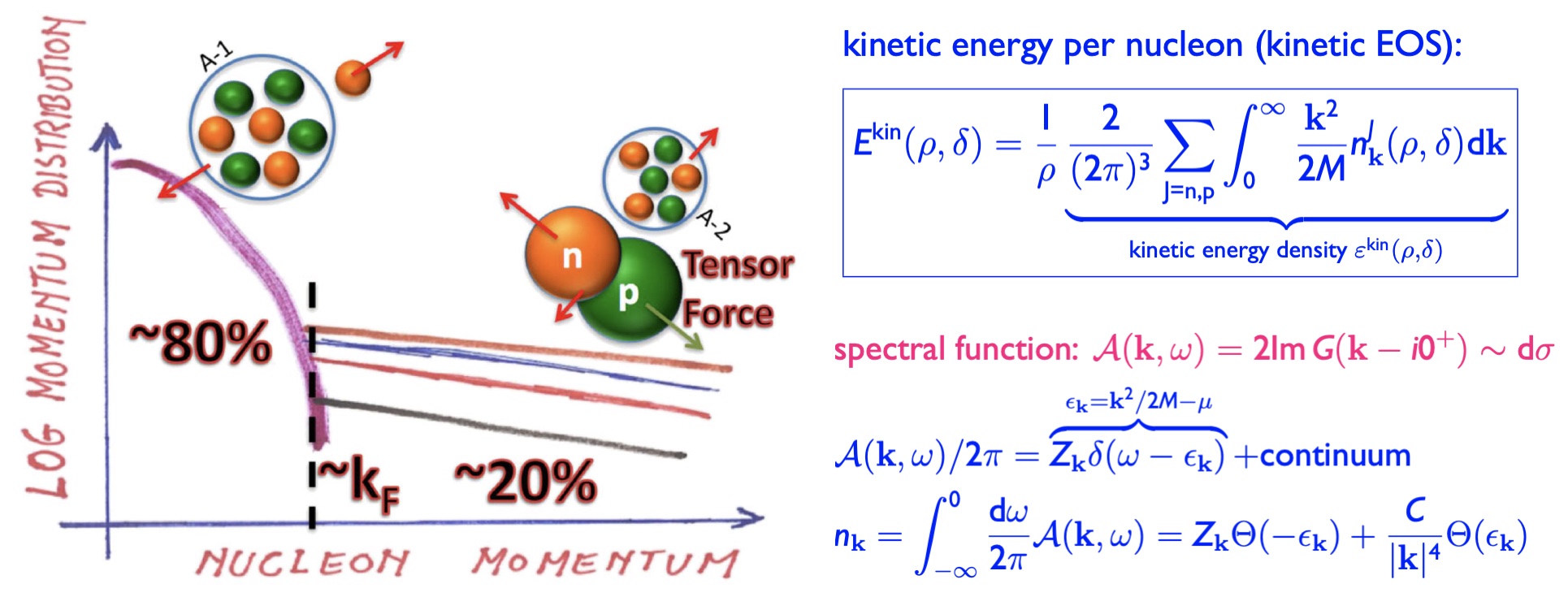
Our group is investigating novel aspects of NN-SRCs and their wide-ranging implications, including the origin and detailed characterization of the high momentum tail in atomic nuclei, the impact of isospin and finite-size effects of the high momentum tail on the equation of state of dense nuclear matter, and the self-consistent inclusion of SRC effects in heavy-ion collision dynamics. Their research also explores how NN-SRCs influence neutron star properties, modify neutrino-nucleus scattering across energy scales, and uncover intriguing parallels with high momentum tail phenomena observed in ultra-cold atomic gases, all with the goal of deepening our understanding of nuclear interactions from microscopic to astrophysical scales and revealing the fundamental principles governing these complex quantum many-body systems.
Related Courses: (1) Quantum Many-body Theories; (2) Nuclear Reaction/Structure Theories.
Dense Matter in Neutron Star Cores under Strong-field Gravity
Neutron stars are cosmic laboratories where gravity, quantum mechanics, and nuclear physics converge. These compact stellar remnants, just 10 to 14 kilometers across but up to twice the mass of the Sun, contain matter at densities far beyond that of atomic nuclei. Understanding their internal composition is a fundamental challenge that touches on the limits of the strong nuclear force, the possibility of exotic phases like quark matter, and the true nature of dense matter. A central goal in neutron star physics is to determine the equation of state, how pressure depends on energy density, deep inside the star. A key quantity in this context is the speed of sound, which encodes the stiffness of dense matter and directly affects the maximum mass and compactness of neutron stars. Unusual features in the speed of sound profile may indicate phase transitions or new forms of matter under extreme conditions. Recent advances in astrophysical observations have revolutionized our ability to probe neutron star interiors. Gravitational wave events from neutron star mergers, detected by LIGO and Virgo, provide constraints on tidal deformability. Simultaneously, high-precision X-ray timing from NASA’s NICER mission and the upcoming Chinese-European eXTP mission offer mass–radius measurements that are sensitive to the equation of state. These data require equally sophisticated theoretical tools for interpretation.

Recently, Dr. Cai and his collaborators developed the IPAD-TOV method (Intrinsic and Perturbative Analyses of the Dimensionless Tolman–Oppenheimer–Volkoff equations), offering a novel and model-independent framework to probe the deep interiors of neutron stars. By reformulating the TOV equations in a fully dimensionless and intrinsic form, IPAD-TOV isolates the core physical features of neutron star structure, revealing universal relations among pressure, energy density, compactness, and the trace of the energy-momentum tensor. Most notably, it enables the direct extraction of the central equation of state (EOS) from astrophysical observations, without relying on specific nuclear models. This flexible framework can be extended to study rotating neutron stars, their transport properties such as thermal conduction and shear viscosity, as well as the influence of intense magnetic fields that may reach up to 10¹⁵–10¹⁸ Gauss in magnetars. These extreme magnetic fields can significantly alter the microphysics of dense matter, impacting the EOS, modifying particle populations, and introducing anisotropies in pressure and transport coefficients. The IPAD-TOV approach thus opens new avenues to systematically investigate how strong-field gravity and magnetism interplay with quantum many-body physics in the densest environments known. As precision data from LIGO, NICER, and the upcoming eXTP mission continue to sharpen our observational lens, the IPAD-TOV method provides a powerful theoretical bridge, connecting multi-messenger astronomy with the fundamental physics of the strong nuclear interaction, phase transitions, and the exotic states of matter that emerge at supranuclear densities. Figure taken from Bao-Jun Cai and Bao-An Li, EPJA, 61, 55 (2025).
Related Courses: (1) General Relativity; (2) Physics of Compact Stars; (3) Black Hole Perturbation Theories.
Relativistic Nuclear Many-body Problems via Quantum Hadrodynamics
While non-relativistic nuclear models have laid important groundwork in describing low-energy nuclear phenomena, they inherently fall short when confronted with the complexities of dense and relativistic nuclear systems. They fail to naturally explain the saturation of nuclear matter, underestimate the magnitude of spin-orbit splitting in finite nuclei, and break down in regimes of high density and energy, such as those encountered in neutron stars and heavy-ion collisions. In contrast, QHD, introduced through the seminal Walecka model, offers a powerful relativistic field-theoretical framework that captures the essential dynamics of nuclear matter. By modeling nucleons as Dirac particles interacting via meson exchange—most notably, the attractive scalar (sigma) and repulsive vector (omega) mesons—the Walecka model provides an elegant and physically transparent mechanism for nuclear saturation and the emergence of realistic spin-orbit interactions. Extensions of the model incorporate isovector mesons (such as the rho) and nonlinear self-interactions, enabling accurate descriptions of asymmetric matter and high-density environments. More profoundly, QHD captures many emergent features anticipated from QCD in its non-perturbative regime, including effective hadronic degrees of freedom, spontaneous symmetry breaking, and in-medium modifications of masses and couplings. In this sense, the Walecka model not only remedies the deficiencies of non-relativistic approaches but also stands as a vital bridge between fundamental QCD and the phenomenology of finite nuclei, nuclear matter, and astrophysical compact objects. Figures taken from B. Serot and J. Walecka, Adv. Nucl. Phys., 16, 1 (1986).
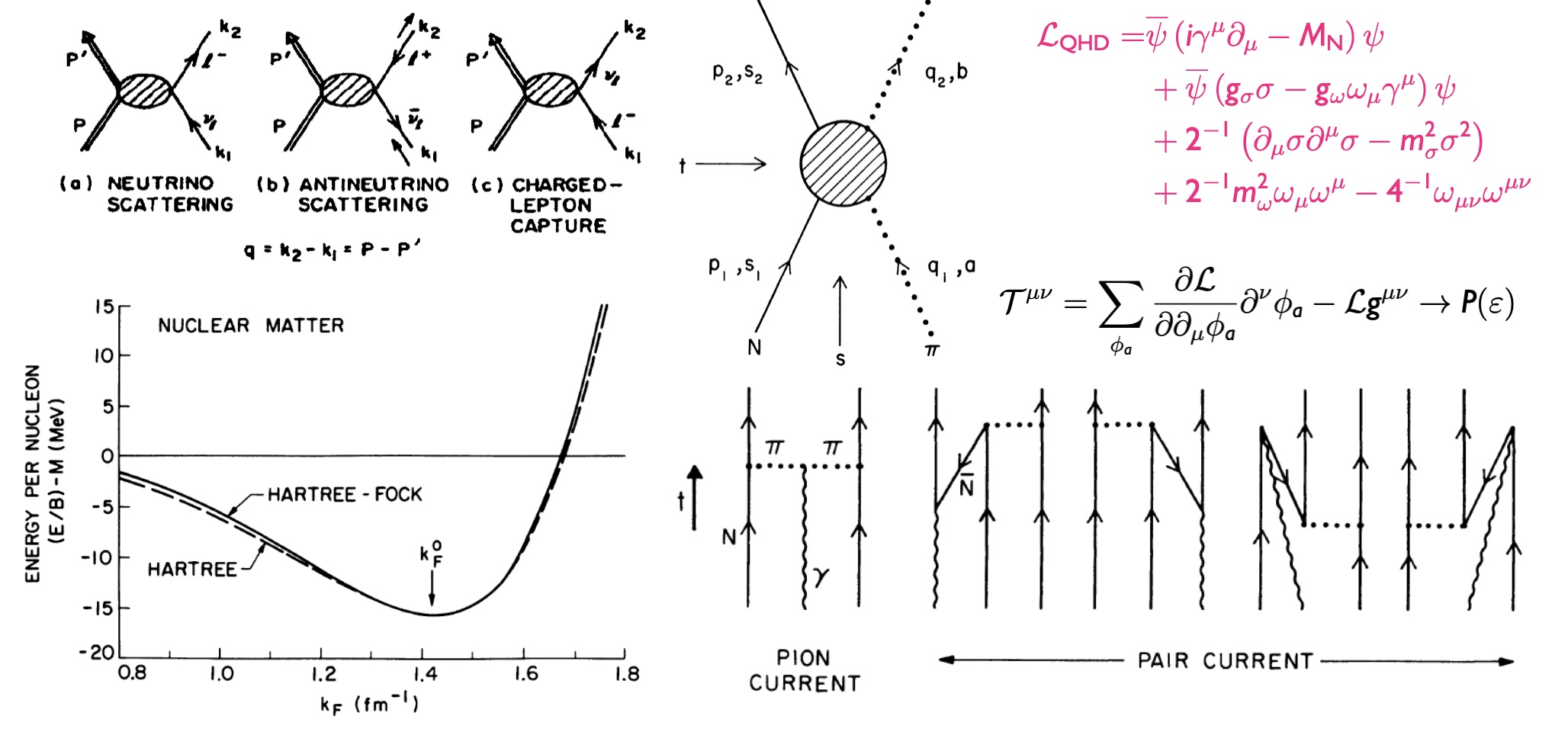
Building on the powerful framework of QHD, our group is advancing a series of in-depth investigations to bridge fundamental nuclear theory with frontier astrophysical phenomena. Their goals include: (1) constructing a unified and realistic equation of state based on QHD that spans from normal nuclear densities to the extreme conditions inside neutron stars, with particular attention to the behavior of the nuclear symmetry energy and consistency with both terrestrial experiments and astrophysical observations; (2) incorporating exotic degrees of freedom, such as hyperons, Delta resonances, and potential dark matter components, into the QHD framework to explore their impact on dense matter properties and neutron star composition; (3) developing a microscopic understanding of the momentum dependence of the single-nucleon potential, a key input for transport models in heavy-ion collisions and nuclear reactions; (4) going beyond the mean-field level by including quantum corrections, correlations, and fluctuations that become increasingly important in dense and dynamic environments; and (5) extending the formalism to include neutrino–nucleus and more general electroweak interactions, with implications for both laboratory experiments and astrophysical processes such as supernovae and neutron star cooling. Through these efforts, the group aims to enrich the theoretical foundations of dense matter physics and deepen the connection between nuclear microphysics and multi-messenger astrophysics.
Related Courses: (1) Relativistic Nuclear Many-body Theories; (2) Neutrino Physics.
Low-density Isospin Asymmetric Nuclear Matter from QCD Sum Rules
The QCD sum rules method is a powerful non-perturbative framework for probing hadronic properties directly from the fundamental theory of strong interactions. Pioneered by Shifman, Vainshtein, and Zakharov in the 1970s, this method bridges the gap between the microscopic world of quarks and gluons and the macroscopic observables of hadron physics. At its heart lies the operator product expansion, which disentangles short-distance (perturbative) contributions, treatable via perturbative QCD, from long-distance (non-perturbative) dynamics encoded in vacuum condensates, such as quark and gluon condensates. These condensates capture the complexity of the QCD vacuum and embody the profound idea that hadrons are not merely bound states of valence quarks, but also shaped by the rich quantum structure of the vacuum itself. The method constructs dispersion relations for two-point correlation functions of quark currents, linking their theoretical (QCD) and phenomenological (hadronic) representations. A Borel transformation is applied to suppress continuum contributions and enhance sensitivity to the ground state, making the extraction of hadron masses, decay constants, and medium modifications feasible. As a semi-analytic tool that reflects the core principles of QCD, the sum rules method has become a cornerstone in hadron spectroscopy, nuclear matter studies, and investigations of hot and dense QCD matter. Figures taken from M. Shifman et al., NPB, 147, 385 (1978), Bao-Jun Cai and Lie-Wen Chen, PRC, 024303 (2021).

Building on Dr. Cai’s early application of QCD sum rules to the equation of state of isospin asymmetric and pure neutron matter, anchored in the fundamental Hugenholtz–Van Hove theorem, this framework provides a powerful means to trace the QCD origins of key uncertainties in nuclear matter properties. Conversely, precise knowledge of the equation of state from experiments, astrophysical observations, and model-independent calculations can constrain in-medium quark and gluon condensates, offering insight into partial chiral symmetry restoration and hadronic modifications. Important future directions include (1) better understanding the in-medium behavior of four-quark condensates, which currently rely on effective interpolation but need more fundamental treatment to reduce uncertainties; (2) systematically investigating many-body interactions, especially nucleon three-body forces, to improve saturation properties and the density dependence of symmetry energy; (3) exploring innovations like complex-valued Borel transformations to enhance spectral function resolution and extend predictions to higher densities; and (4) applying QCD sum rules combined with methods such as the scheme of maximum entropy to study universal low-density neutron matter resembling a unitary Fermi gas, focusing on the imaginary parts of self-energies and transport coefficients. Collectively, these efforts aim to develop QCD sum rules into a more predictive and versatile tool for probing strongly interacting nuclear matter from first principles.
Related Courses: (1) Perturbative Quantum Field Theory; (2) Nuclear Many-body Physics; (3) Ultra-cold Atomic Physics.
Effective Nuclear Systems in Low Spatial Dimensions
Dimensionality, defined as the number of independent coordinates or degrees of freedom required to describe a system, lies at the heart of modern physics, data science, and beyond. In physics, exploring systems beyond the familiar three dimensions has revealed deep insights and novel phenomena. Landmark developments, such as dimensional regularization in quantum field theory and the renormalization group theory of second-order phase transitions, demonstrate how treating space-time dimension as a continuous variable leads to powerful analytic tools and effective field theories. In statistical and condensed matter physics, the exact solution of the 2D Ising model and the emergence of critical phenomena exemplify the profound role dimensionality plays in organizing universal behavior. Recent advances in ultracold atomic gases have opened a unique window into low-dimensional quantum matter. Enabled by technologies such as Feshbach resonances, optical lattices, and artificial gauge fields, experiments in 1D and 2D geometries have revealed exotic behavior: scale anomalies, spin-charge separation, generalized hydrodynamics, and novel non-Hermitian phase transitions. These platforms serve as quantum simulators for many-body systems, offering precision tests of theories across dimensions.
In nuclear physics and astrophysics, dimensionality is emerging as a key conceptual tool. Though traditionally treated in three dimensions, systems such as finite nuclei, heavy-ion collisions, and neutron stars can exhibit effectively reduced dimensionalities due to symmetries, topologies, or geometric constraints. For instance, toroidal nuclei and bubble nuclei, particle jets in heavy-ion collisions, or the thin crust and radially symmetric core of neutron stars suggest quasi-2D or quasi-1D behavior. These perspectives raise the question: can the nuclear equation of state, particularly for asymmetric nucleonic matter, be generalized to arbitrary dimensions to capture deeper organizing principles? Understanding such issues in reduced dimensions may reveal novel thermodynamic or transport properties relevant for neutron star structure, core-crust transitions, and supernova dynamics.
Beyond physics, the idea of dimensionality also plays a foundational role in data science. High-dimensional data often lies on low-dimensional manifolds, and techniques like principal component analysis aim to extract such effective dimensional structures. This parallel hints at a unifying principle: in both physical and informational systems, emergent simplicity often resides in reduced dimensional representations, where critical information is retained while complexity is suppressed. Together, these developments suggest that dimensionality is not merely a geometric property, but a deep organizing principle that governs universality, criticality, and effective description across disciplines. Studying many-body systems across general dimensions may not only expand theoretical reach but also unify insights from seemingly disparate fields such as ultracold gases, nuclear matter, astrophysics, and machine learning.
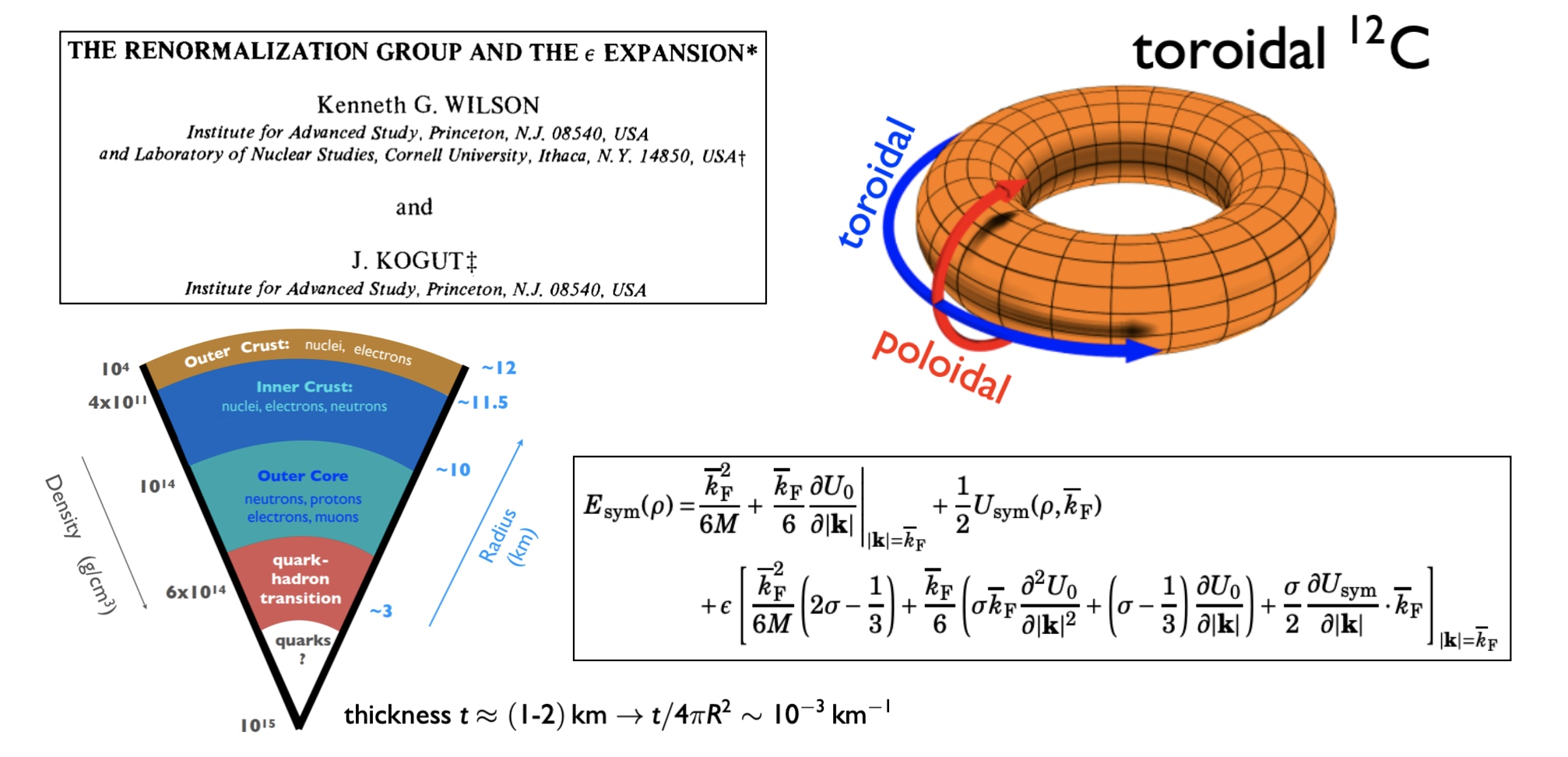
Together with his collaborators, Dr. Cai studied and presented a novel generalization of the equation of state for asymmetric nuclear matter by extending the Hugenholtz–Van Hove theorem to arbitrary spatial dimensions. This dimensional framework yields analytic expressions for kinetic terms, symmetry energy, and its density derivatives, uncovering near-universal scaling behaviors. Notably, the symmetry energy and its slope grow approximately linearly with dimension, while key ratios remain strikingly stable, highlighting deep geometric effects shaping dense matter. As the spatial dimension decreases, the system naturally approaches the behavior of a free Fermi gas despite strong short-range nucleon correlations, implying that geometry alone can mimic complex interaction phenomena, beyond the well-known effects of quantum statistics.
Looking forward, our group try to (1) gain fresh insights into exotic low-dimensional nuclear structures such as nuclear pasta phases in neutron star crusts, improving understanding of their mechanical and transport properties; (2) sharpen predictions of neutron star macroscopic properties including mass, radius, and moment of inertia by embedding geometric constraints into the dense matter description; (3) develop frameworks to explore nonequilibrium and anisotropic conditions in core-collapse supernovae, potentially enhancing models of neutrino transport and explosion dynamics; (4) disentangle and better understand universal features and empirical correlations across finite nuclei and neutron stars by varying spatial dimension; (5) extend this framework to relativistic regimes to unify microscopic nuclear physics with gravitational observations, placing tighter constraints on neutron star interiors and merger remnants; and (6) investigate whether deep theoretical principles govern low-dimensional nuclear systems, potentially revealing fundamental symmetries or emergent phenomena yet to be uncovered. Together, these efforts may open a new avenue that geometrizes dense matter and deepens the connection between symmetry, dimension, and the extraordinary astrophysical phenomena shaping our universe.
Related Courses: (1) Ultra-cold Atomic Physics; (2) Quantum Statistical Physics (Renormalization Group and epsilon Expansion).
Data Science, Large-scale Optimization and Learning Algorithms
Recent advances in data science and large-scale optimization have ushered in a new era of intelligent systems, driven by powerful learning architectures such as deep neural networks, transformers, and diffusion models. These modern frameworks have transformed diverse fields, including machine learning, computer vision, computer graphics, and bioinformatics, by enabling automatic pattern discovery, semantic understanding, high-resolution image synthesis, and molecular structure prediction. Beyond computational breakthroughs, these algorithms have reshaped scientific workflows by turning massive datasets into predictive models, offering new perspectives and augmenting human intuition.
In the realm of nuclear physics and astrophysics, data-driven approaches are increasingly essential for probing the structure of matter under extreme conditions and for interpreting signals from the universe. Machine learning techniques enable the acceleration of many-body calculations, the identification of phase transitions in strongly correlated systems, and the constraint of nuclear interactions from experimental data. In heavy-ion collisions, where petabytes of data are generated, modern algorithms play a crucial role in extracting rare and subtle signals hidden within overwhelming backgrounds. In astrophysics, learning-based methods assist in decoding gravitational waveforms, modeling neutron star mergers, and analyzing high-dimensional data from observatories. As theoretical models and observational datasets grow in complexity, the fusion of modern algorithms with fundamental physics offers transformative potential for uncovering the deep laws of nature.
Our group aims to study frontier problems in nuclear physics and astrophysics by integrating advanced data-driven and optimization techniques. Their research directions include: (1) applying modern Bayesian inference frameworks, such as Bayesian model averaging and mixing, to rigorously quantify uncertainties in theoretical predictions; (2) developing accurate and efficient optimization algorithms inspired by statistical physics, tailored for complex physical systems; (3) uncovering intrinsic low-dimensional structures hidden within high-dimensional datasets using techniques like principal component analysis, singular value decomposition, sparsity-based methods such as LASSO, and modern tools from high-dimensional statistics and random matrix theory; (4) leveraging matrix factorization and advanced linear algebra to efficiently simulate large-scale physical systems exhibiting certain symmetry; (5) designing computational strategies to model shock wave phenomena in extreme astrophysical events such as neutron star mergers and supernova explosions; (6) employing fast randomized algorithms to enable approximate yet tractable solutions to otherwise computationally prohibitive problems and extremely large datasets; and (7) exploring the deep principles behind the effectiveness of modern neural networks, drawing inspiration from statistical physics concepts like the renormalization group and effective field theories. The group seeks to bridge data science and theoretical modeling, offering new perspectives on the fundamental physics of dense matter and violent cosmic events.
Related Courses: (1) First-order and Second-order Optimizations; (2) Matrix Computations; (3) Bayesian Inference; (4) Algorithms and Randomized Design.
